Paper Clips [B]

Memory limit: 64 MB

Small Bytedragon recently discovered a great game - building chains out of paper clips. One day he constructed a long-long chain made of his father's paper clips and he went to school. Unfortunately for Bytedragon, his father needs all of his paper clips. As one may expect, he needs all of them... separated. However, before he starts to disassemble son's construction, he wants to know how long would it take.

Dad is going to untangle the chain by performing moves of rotating one paper clip by 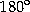around its axis perpendicular to the surface of the table. Each move takes exactly one second. The image below demonstrates performing of some single moves against small paper clip chain.

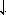
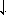
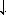
Fig. 1: A few first moves of the process of untangling the chain.

Task

Write a program which:

• reads a description of the chain from the standard input,
• computes the minimal number of moves required to untangle the chain,
• writes the result to the standard output.

Input

The chain is described by the alignment of its consecutive links and the connection type between each consecutive pair. When looking from above at the paper clip laying on the table we can see it in one of four possible positions, just as the image below shows.

(A)	(B)	(C)	(D)

Fig. 2: Four possible positions of the paper clip on the table.

Two paper clips are connected in one of two possible ways - top part of the left paper clip goes above top part of the right paper clip or vice versa.

Both situations are presented in the image below.

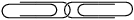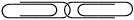(P)	(Q)

Fig. 3: Two possible links of the paper clips presented on the base of the pair BA.

In the first line of the input there is one integer (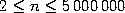) representing the number of paper clips. In the second line there is a description of the chain consisting of letters A, B, C, D, P and Q. Letters represent arrangement of the paper clips and the way of connection of the consecutive pairs.

Output

In the first and only line of the output there should be one integer - the minimal number of moves required to separate chain into single paper clips.

Example

For the input data:

5
CPBQAPAPB

the correct result is:

4

In the example the initial chain looks like the one from the figure 1. It can be disassembled in four moves, if one behaves differently from the process depicted on that image.

Task author: Szymon Acedanski.